自变量x和因变量y有如下关系:
y=kx (k为任意不为零实数) 或y=kx+b (k为任意不为零实数,b为任意实数) 则此时称y是x的一次函数。 特别的,当b=0时,y是x的正比例函数。正比例是Y=kx+b。 即:y=kx (k为任意不为零实数)
定义域: 自变量的取值范围,自变量的取值应使函数有意义;要与实际相符合 一次函数的性质
1.y的变化值与对应的x的变化值成正比例,比值为k 即:y=kx+b(k≠0) (k为任意不为零的实数 b取任何实数)
2.当x=0时,b为函数在y轴上的截距。
3.k为一次函数y=kx+b的斜率,k=tg角1(角1为一次函数图象与x轴正方向夹角) 形。取。象。交。减
4.正比例函数也是一次函数.
5.当k相同,图像平行;当k不同,图像相交
一次函数的图像及性质
1.作法与图形:通过如下3个步骤
(1)列表[一般取两个点,根据两点确定一条直线];
(2)描点;
(3)连线,可以作出一次函数的图像——一条直线。因此,作一次函数的图像只需知道2点,并连成直线即可。(通常找函数图像与x轴和y轴的交点)
2.性质: (1)在一次函数上的任意一点P(x,y),都满足等式:y=kx+b(k≠0)。 (2)一次函数与y轴交点的坐标总是(0,b),与x轴总是交于(-b/k,0)正比例函数的图像都是过原点。
3.函数不是数,它是指某一变量过程中两个变量之间的关系。
4.k,b与函数图像所在象限:
y=kx时(即b等于0,y与x成正比)
当k>0时,直线必通过一、三象限,y随x的增大而增大;
当k<0时,直线必通过二、四象限,y随x的增大而减小。
y=kx+b时:
当 k>0,b>0, 这时此函数的图象经过一,二,三象限。
当 k>0,b<0, 这时此函数的图象经过一,三,四象限。
当 k<0,b>0, 这时此函数的图象经过一,二,四象限。
当 k<0,b<0, 这时此函数的图象经过二,三,四象限。
当b>0时,直线必通过一、二象限;
当b<0时,直线必通过三、四象限。
特别地,当b=0时,直线通过原点O(0,0)表示的是正比例函数的图像。
这时,当k>0时,直线只通过一、三象限;当k<0时,直线只通过二、四象限。
4、特殊位置关系
当平面直角坐标系中两直线平行时,其函数解析式中K值(即一次项系数)相等
当平面直角坐标系中两直线垂直时,其函数解析式中K值互为负倒数(即两个K值的乘积为-1)
确定一次函数的表达式
已知点A(x1,y1);B(x2,y2),请确定过点A、B的一次函数的表达式。
(1)设一次函数的表达式(也叫解析式)为y=kx+b。
(2)因为在一次函数上的任意一点P(x,y),都满足等式y=kx+b。所以可以列出2个方程:y1=kx1+b …… ① 和 y2=kx2+b …… ②
(3)解这个二元一次方程,得到k,b的值。
(4)最后得到一次函数的表达式。








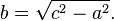
 ,其中的
,其中的 称为勾股数。例如
称为勾股数。例如 就是一組勾股數組。
就是一組勾股數組。 ,其中
,其中 。
。