勾股定理

（英语：Pythagorean theorem）又称商高定理、畢達哥拉斯定理、毕氏定理、百牛定理，是平面几何中一个基本而重要的定理。勾股定理说明，平面上的直角三角形的两条直角边的长度（古称勾长、股长）的平方和等于斜边长（古称弦长）的平方。反之，若平面上三角形中两边长的平方和等于第三边边长的平方，则它是直角三角形（直角所对的边是第三边）。

勾股定理 是人类早期发现并证明的重要数学定理之一。

据《周髀算經》中记述，公元前一千多年周公与商高论数的对话中，商高就以三四五3个特定数为例详细解释了勾股定理要素，其一，“以为句广三，股修四，径隅五”。其二，“既方其外，半之一矩，环而共盘，得成三四五。两矩共长二十有五，是谓积矩。”首先肯定一个底宽为三，高为四的直角三角形，弦长必定是五。最重要的是紧接着论证了弦长平方必定是两直角边的平方和，确立了直角三角形两条直角边的平方和等于斜边平方的判定原则。其判定方法后世不明其法而被忽略。^[1]。

此外，《周髀算经》中明确记载了周公后人陈子叙述的勾股定理公式：“若求邪至日者，以日下为勾，日高为股，勾股各自乘，并而开方除之，得邪至日”。

赵爽在《周髀算經注》中将勾股定理表述为“勾股各自乘，并之，为弦实。开方除之，即弦。”。

古埃及在公元前2600年的纸莎草就有（3,4,5）这一组勾股数，而古巴比伦泥板涉及的最大的一个勾股数组是（18541，12709，13500）。

古希腊发现勾股定理的是毕达哥拉斯，所以勾股定理又称畢達哥拉斯定理。據說畢達哥拉斯證明了這個定理後，即斬了百頭牛作慶祝（百牛大祭），因此又稱百牛定理。但这个说法显然是以讹传讹，众所周知毕达哥拉斯主义者在古代以素食闻名。^[2]

有些參考資料提到法国和比利時將勾股定理称为驴桥定理，但驴桥定理就是等邊對等角，是指等腰三角形的二底角相等，非勾股定理

定理

在平面上的一個直角三角形中，两个直角边边长的平方加起来等于斜邊长的平方。如果设直角三角形的两条直角边长度分别是a和b，斜边长度是c，那么可以用数学语言表达：

勾股定理是餘弦定理中的一個特例^[4]。勾股定理現約有400種證明方法，是數學定理中證明方法最多的定理之一^[5]。

其他形式[编辑]

如果c是斜邊的長度而a和b是另外兩條邊的長度，勾股定理可以寫成：

如果a和b知道，c可以這樣寫：

如果斜邊的長度c和其中一條邊（a或b）知道，那另一邊的長度可以這樣計算：

或

勾股數组[编辑]

主条目：勾股數

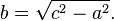
勾股数组是滿足勾股定理的正整數組，其中的称为勾股数。例如就是一組勾股數組。

任意一组勾股数可以表示为如下形式：，其中。